JAPANESE / ENGLISH

JAPANESE / ENGLISH
Last updated on 05/7/2021
Total Internal Reflection (TIR) is a phenomenon in optics, by which light experiences complete reflection at an interface between two media. Most optical fibers use TIR as the guiding principle. Figure 1 explains schematically how TIR takes place at an interface between two media. When an incident light ray (red) hits the interface, it is reflected (green) and/or refracted (blue).
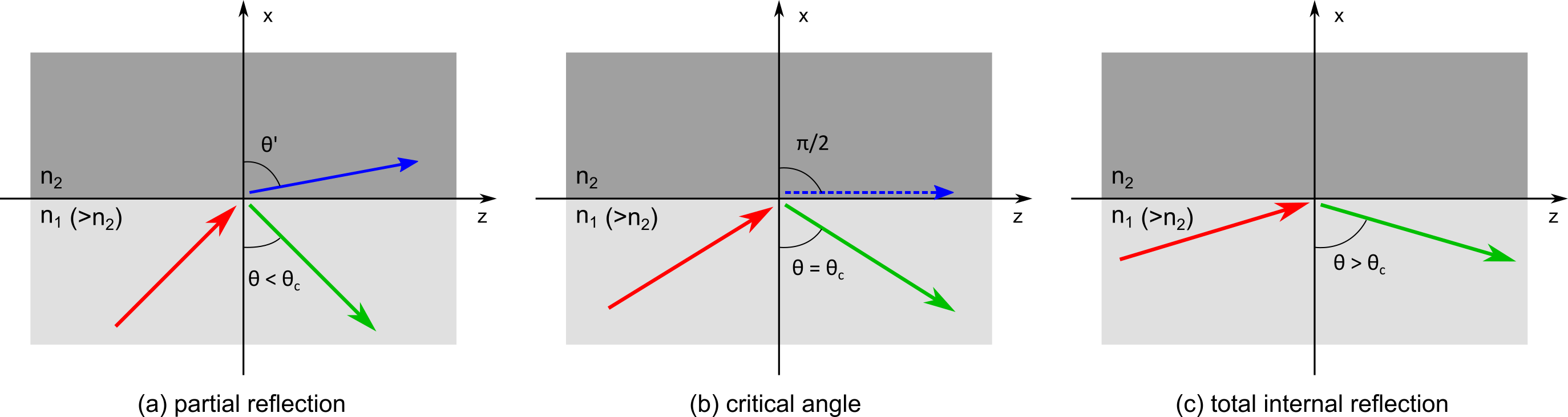
Figure 1: Snell’s law and total internal reflection.
The angle of refraction at the interface of two materials is given by Snell’s law:
\(\displaystyle \mathrm{n_1}\cdot \sin(\theta) = \mathrm{n_2} \cdot \sin(\theta^{\prime}), \)
where n1 and n2 are the refractive indices of the two materials, θ is the incident angle of light, and θ’ is the angle of refraction [see Figure 1(a)]. If we assume that material 1 is water (n1=1.3) and material 2 is air (n2=1.0), θ’ is larger than θ as n1>n2, and θ’ becomes \(\pi\) /2 (i.e. 90 deg) for a certain incident angle θ = θc [Figure 1(b)]. This angle is called the critical angle, and is given by the following formula:
\(\displaystyle \theta_{\mathrm{c}}=\sin^{-1}\left( \frac{\mathrm{n_2}}{\mathrm{n_1}} \right). \)
And at an incident angle θ > θc [Figure 1(c)], the refracted light can no longer exist, and light is totally reflected back to the material 1 (water).
This phenomenon can also be understood intuitively, when you dive into a swimming pool and try to see above the water surface – you cannot see above the water with a shallow angle.