JAPANESE / ENGLISH

JAPANESE / ENGLISH
Last updated on 05/7/2021
Understanding light propagation in an optical fiber by ray optics gives an intuitive understanding and, in fact, is a good approximation if the size of the core is much larger than the wavelength guided in the optical fiber. The electromagnetic properties of an optical fiber, however, become essential as the size of the waveguide becomes closer to the wavelength. The concept of modes in an optical waveguide is one of the most important concepts when analyzing an optical fiber using electromagnetics.
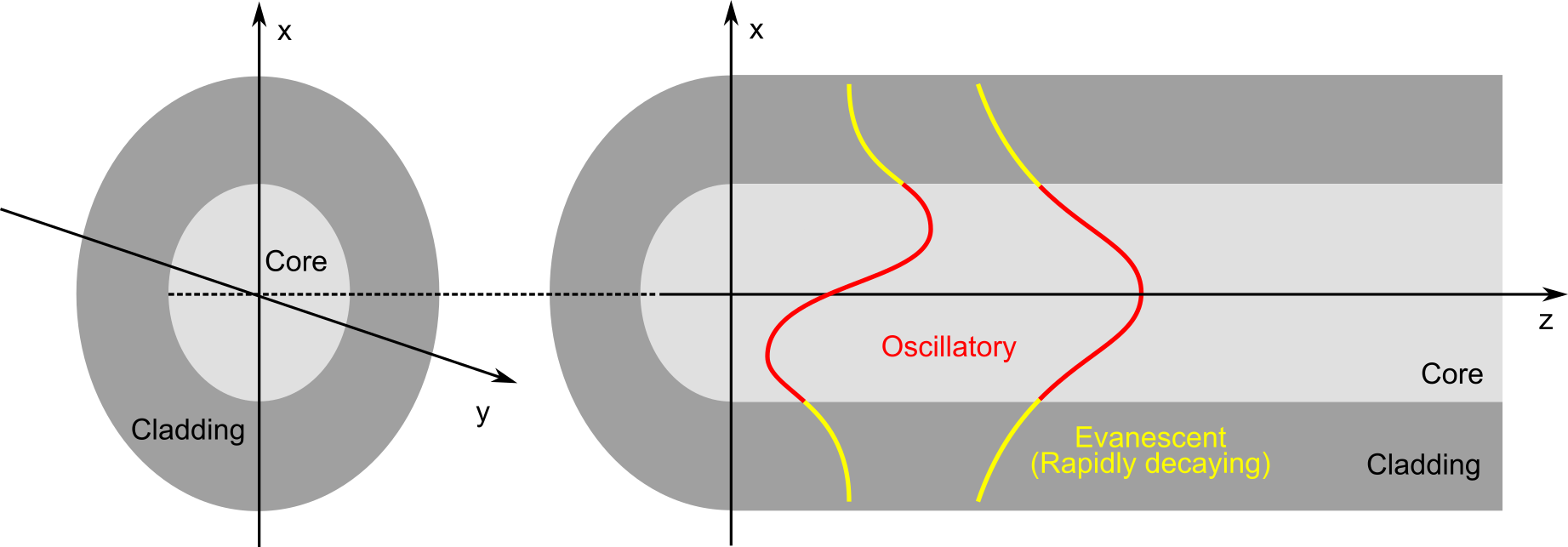
Figure 1: Schematic of optical fiber and guided modes.
Figure 1 shows schematically a longitudinally uniform optical fiber and examples of modes. Each mode maintains the distribution of the electromagnetic field in the x-y plane (modal-field distribution) as it propagates in the z-direction. Modes are determined once the refractive-index profile and the angular frequency of light \(\omega\) (\(\omega=2\pi C_0/\lambda\) where \(C_0\) is the speed of light in vacuum) are given, the electromagnetic field of the mode at an arbitrary position and time is given as follows:
\(\displaystyle \mathbf{E}_{\beta}(x,y,z,t)=\mathbf{E}_{\beta}(x,y)e^{i(\omega t – \beta z)}, \) \( \mathbf{H}_{\beta}(x,y,z,t)=\mathbf{H}_{\beta}(x,y)e^{i(\omega t – \beta z)}. \)
The propagation constant \(\beta\) of each mode is provided by solving an eigenvalue problem (which is determined by the refractive-index profile and angular frequency \(\omega\)), and the modal-field distribution \(\mathbf{E}_{\beta}(x,y)\) or \(\mathbf{H}_{\beta}(x,y)\) is the eigenstate for the eigenvalue.
The modal-field distribution is generally either oscillatory or evanescent in the transverse direction. If the modal-field distribution is oscillatory in the core and evanescent in the cladding, the mode is confined in the core as the modal-field distribution rapidly decays in the cladding. These modes are referred to as guided modes. Guided mode is the most important type of modes and is often simply referred to as “mode”.
A set of guided modes with the same (or very close) \(\beta\) generally show very similar characteristics (e.g. modal-field distribution) except their polarization states; this set of modes is called a mode class. An optical fiber with a large core guides multiple mode classes and the fiber is called a multimode fiber. The number of mode classes reduces as the size of the core decreases, and when the size becomes sufficiently small, only one mode class is allowed. This fiber is called a single-mode fiber.